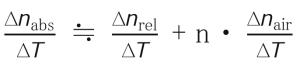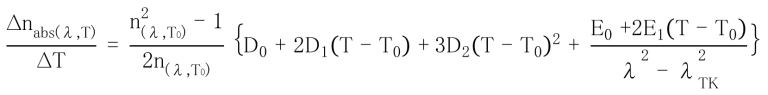| Date |
Ref |
Description |
| 18 Apr, 2025 |
PBM2R |
Radiation-resistant optical glass PBM2R (Radiation Resistant Glass Types) |
| 18 Apr, 2025 |
Catalog Data Update |
Notice of Catalog Data Update for Temperature Coefficient of Refractive Index Δn/ΔT "Read More" |
| 18 Apr, 2025 |
Measurement Equipment |
Renewal of Thermal Expansion Measurement Equipment | … all the average coefficient of linear expansion [α], transition point [Tg], and yield point [At] values on our website have been changed with the 2025 catalog update. "Read More" |
| 07 Feb, 2025 |
Fused Silica |
SK1300 and SK1310 PDF datasheets updated. |
| 30 Jan, 2025 |
S-TIH53WN
S-LAH66N
S-LAL18N |
Introducing S-TIH53WN, S-LAH66N, and S-LAL18N: Meeting High-Precision Lens Demands |
| 06 Jan, 2025 |
LICGC AG-01 |
Notice of Discontinuation: LICGC AG-01 Plates have been discontinued (limited stock may be available upon request). |
| 28 Oct, 2024 |
i-Line Glass |
PDF Datasheets to reflect changes to photoelastic constant [β] values. |
| 29 Feb, 2024 |
National Geographic E6 Glass |
Ohara’s E6 Glass is featured in National Geographic’s The Glass Age. Read More |
| 26 Feb, 2024 |
S-FPL53
S-FPL55 |
PDF Datasheets updated to reflect changes to coloring λ80λ5 and internal transmission λ0.80/λ0.05 values. |
| 02 Feb, 2024 |
S-NBM52 |
New Glass Type! S-NBM52 is a new optical glass for polished lenses with higher dispersion while maintaining the same anomalous dispersion as S-NBM51. Read More |
| 20 Nov, 2023 |
LLNL – NIF |
Ohara optical glass and Fused Silica in the NIF! Read More |
| 06 Oct. 2023 |
U of A – GMT7 |
Ohara’s E6 glass is melted for the Giant Magellan Telescope’s last Primary Mirror, GMT7! Read More |
| 08 May 2023 |
Special Order Glass Types |
Due to low demand, the following glass types will be moved to Special-Order Glass Types and available for the next 3 years: S-BAH10, S-LAH79, L-TIM28P, S-BAL2, S-TIM22, S-TIH23, S-LAL13, S-LAM54, S-LAH63, & S-LAH63Q. Please contact us directly for recommended alternative glass types and additional information. |
| 08 May 2023 |
Discontinued Glass Types |
The following glass types have been discontinued (limited stock may be available upon request): S-FTL10, S-NSL5, S-BAH32, S-TIM39, S-LAM52, S-LAM58, S-YGH51, S-NBH52, S-NBH53, S-TIM1, SNPH53, & L-LAH86. |
| 13 Jan. 2023 |
S-LAL61Q |
New Glass Type! S-LAL61Q is a new optical glass for polished lenses with improved chemical durability and a mechanical strength equivalent to S-LAL61. Read More |
| 30 Nov. 2022 |
S-LAH99W |
New Glass Type! S-LAH99W is an optical glass with an improved transmittance version of S-LAH99. Read More |
| 27 Dec. 2021 |
S-NBH59 |
New Glass Type! S-NBH59 is an optical glass for polishing lens and is effective for secondary chromatic aberration correction. Read More |
| 18 Feb. 2021 |
Mars Rover |
Ohara Glass Lands on Mars! Read More |
| 03 Dec. 2020 |
Discontinued Glass Types |
The following glass types have been discontinued (limited stock may be available upon request): S-BAH32, S-BAL11, S-BAL41, S-BAM3, S-BSM9, S-BSM22, S-LAL7, S-LAL54, S-LAL56, S-LAM51, S-LAM52, S-LAM58, S-LAM59, S-LAM61, S-NBH52, S-NBH53, S-NPH53, S-NSL5, PBH56, S-TIM1, and S-TIM3. |
| 30 Nov. 2020 |
S-FPM5 |
New Glass Type! S-FPM5 is an optical glass for polished lenses with a Δn/ΔT close to zero. Read More |
| 06 Mar. 2020 |
S-LAL12Q |
New Glass Type! S-LAL12Q is an optical glass with improved workability and durability. Read More |