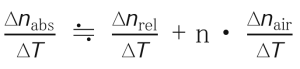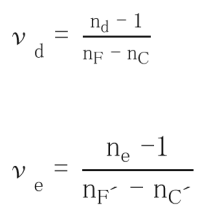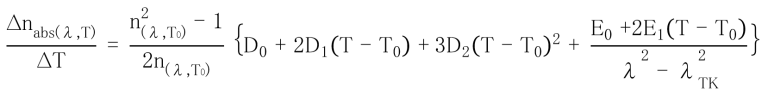Ohara’s E6 Glass is featured in National Geographic
In the February 2024 edition of National Geographic magazine, Ohara’s E6 glass is prominently featured in, “A glass revolution is underway. Spoiler alert: it bends and bounces.”
National Geographic | A Glass Revolution is Underway
National Geographic’s February 2024 issue includes the article, “A glass revolution is underway. Spoiler alert: it bends and bounces,” which features Ohara’s E6 Low Expansion Glass. The article highlights how E6 glass is melted and processed in Japan and serves a pivotal role in the spin-cast mirrors used in several of the world’s largest telescopes. National Geographic emphasizes that E6 glass is just one example of how glass is being reinvented to make huge technological and industrial advancements.
As a multi-decade supplier to The University of Arizona, Ohara has provided more than 200,000 kgs of E6 glass for numerous telescope projects, including the MMT, the Magellan Telescope, the Large Binocular Telescope, and the Giant Magellan Telescope.


Ohara’s E6 glass is heated with a blowtorch, causing the
boule to split. Credit: Christopher Payne/National Geographic.
Photo Overview

19 tons of E6 glass are hand-loaded into the spin-casting furnace at the
Univ. of Ariz. Richard F. Caris Mirror Lab. Credit: Christopher Payne/National Geographic.

An 8.4 meter diameter E6 mirror in the Large Binocular Telescope located
on Mount Graham in Arizona. Credit: Christopher Payne/National Geographic.

As seen in “A glass revolution is underway. Spoiler alert: it bends and bounces,” from the February 2024 issue of National Geographic…
“In 1965 a Japanese firm, Ohara Inc., refined the process with its own admixture to develop E6, a so-called low-expansion glass that’s now made for Ohara only.
A single pot, holding about 200 gallons, takes roughly four months to create. First, the clay vessel must be hand sculpted. Then workers pour in a mix of silica, boron oxide, aluminum oxide, and other materials and heat the pot to 2700 degrees Fahrenheit. As it melts, the molten glass must be stirred periodically for more than two days before the pot is placed in a temperature-controlled chamber to cool for two weeks.
Breaking the clay pot removes the outermost layer of glass, leaving behind a pure substance that can be remelted and formed into precise shapes that remain constant even in extreme temperatures—hence, the “low expansion” part of its name. This stability is crucial when you’re trying to build glass mirrors for large telescopes.
The market for such wildly expensive instruments, the kind that let astronomers peer into the deep recesses of space, is limited. So limited that all the E6 produced in the past 42 years has been delivered to a single buyer. A huge amount—134 tons—is for a project that, if successful, will change the way we think about the universe.
E6 is just one example of how glass is being reinvented to explore a range of frontiers. In fact, glass has seen more technological and industrial developments in the past half century than in the previous millennium, prompting the UN in 2022 to recognize glass as the 100 percent recyclable building block most likely to help countries reach sustainable-development goals by 2030.”