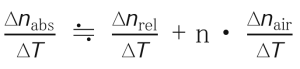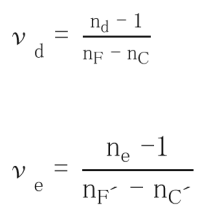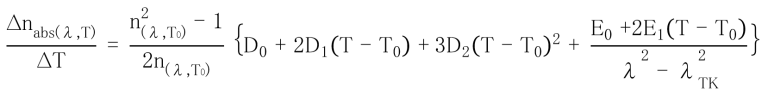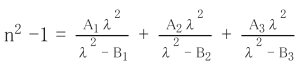|
7.1 Refractive Index and Abbe
|
| Refractive index and Abbe
number values of our fine annealed products vary from catalog value
by: |
| |
|
n d :±0.0005 vd :±0.8% |
| |
| Upon request, we will supply
blanks of optical glass to the following tolerances: Refractive
index : |
| |
|
n d : ±0.0002 vd : ±0.3%
|
| |
| When special demand exists
for specifications with other optical constants than the above,
please consult us. We urge our customers to enjoy the cost savings
and benefits of our close index control, melt to melt, over long
periods of production. Usually this is done at no extra cost. We
normally send certification (melt data) of refractive indices
measured at the spectral lines: C, d, F, g and vd . On special
request, we can supply refractive indices measured at other spectral
lines . The following is the accuracy of standard measurements of
refractive index and dispersion for raw glass and normal pressed
blanks: |
| |
|
Refractive index = ±0.00003 Dispersion
= ±0.00002 |
| |
| On request, we shall provide
precision measurements of refractive index and dispersion:
|
| |
|
Refractive index = ±0.00001 Dispersion
= ±0.000003 |
| |
| We will report
the environmental temperature, humidity and atmospheric pressure of
the room where the precision measurement was undertaken. For,
"ultra-precision measurements" and measurements at spectral lines
not described in this catalog, please contact us. |
| |
|
7.2 Homogeneity
|
It is sometimes necessary to
measure the index variation across a blank. In such cases, Ohara
pays special attention to each process and can supply high
homogeneity "Grade Special A" blanks. Grade Special A is our term
for high homogeneity (Low Δn) optical glasses. Our Grade Special A
glasses are available in the following homogeneity levels:
|
| |
|
Table
|
Classification |
Homogeneity ( Δn) |
|
Grade Special A1 |
±1X10-6 |
| Grade Special
A2 |
±2X10-6 |
| Grade Special
A5 |
±5X10-6 |
| Grade Special A20 |
±20X10-6 | |
| |
Please note that the Grade
Special A number indicates n in the sixth decimal place. The anneal
required must also be specified in terms of birefringence (nm/cm).
Generally, low Δn also implies low birefringence from precision
annealing. Using phase measuring interferometers, we measure
transmitted wave front of each test piece. Interferograms can be
supplied for high homogeneity blanks upon customer
request.
|
| |
|
7.3 Stress Birefringence
|
| Depending on the annealing
condition, optical glass retains slight residual strain in most
cases. This can be observed as optical birefringence, measured by
optical path differences and specified in nm/cm. Stress
birefringence of a rectangular plate is measured at the middle of
the long side where maximum values occur at a point 5% of the width
from the edge. A disc is measured at 4 points located 5% from the
edge of the diameter. The maximum value of the 4 points is shown as
the Birefringence value. We guarantee the strain according to the
grade of anneal as follows: |
| |
|
Table 2 |
| Class |
1 (Precision) |
2 (Fine) |
3 (Course) |
4 (Very
Course) |
| Birefringence
(nm/cm) |
<5 |
<10 |
<20 |
>20
|
Birefringence
Measurement Chart (BMC) can be supplied upon customer
request.
|
| |
|
7.4
Striae |
| Striae are thread-like veins
or cords which are visual indications of abruptly varying density.
Striae can also be considered to be a lack of homogeneity caused by
incomplete stirring of the molten glass. Some glasses contain
components that evaporate during melting, causing layers of varying
density, and therefore parallel striae appear. Striae in glass are
detected by means of a striaescope, which consists of a point source
of light and a collimating lens. Polished samples are examined at
several different angles in the striaescope. They are then compared
with the standards and graded. These established standard glasses
are of a high order of quality and are certified to U.S. military
specification MIL-G-174B. |
| |
|
Table 3 |
| Striae Grade |
Striae Grade Striae Content
Using Striaescope |
|
A
B
C |
No visible striae
Striae is light and scattered
Striae is heavier than Grade B
|
|
| |
|
7.5 Bubbles |
| |
| > Bubble
content is determined by taking a sample of glass from each melt.
The total bubble cross-section per 100ml of glass volume is
measured. Please refer to 6.1 . On
request, we shall undertake bubble examination with the method and
procedures of MIL-G-174B or the customer's own specifications. |
| |
|
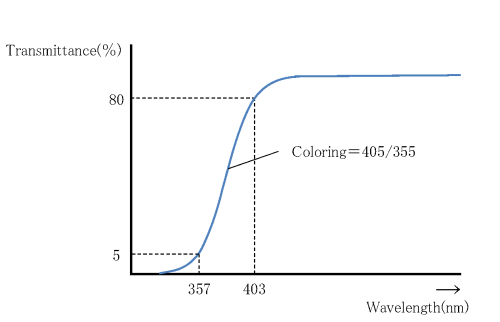
7.6 Coloring |
| Variation of
coloring between melts is generally within ±10 nm. On special
request, we shall report the coloring or the transmission, including
reflection losses, of the melt to be supplied by measuring spectral
transmission. |
| |
|
7.7 Other |
| We showed
each properties as representative value except for 7.1~7.6. Please
contact us when you want to know the other value. In addition,
please let us know your preferred specification when you place the
orders. |
