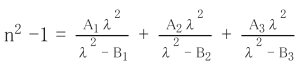4. Chemical Properties
There are some glasses that lack durability due to the chemical behavior of the constituents utilized in the composition. These glasses are influenced by water vapor, acid, gasses, etc., as well as ions in the polishing slurry. Consequently, dimming and staining will occur on the surfaces of these glasses during processing and storage. Since such phenomena have to do with surface conditions and environment, no single test can be accepted as a criterion of durability under all conditions. We listed resistance to water and acid by the powder test method and resistance to weather by the surface test method. We have also listed resistance to acid and phosphate, following the test method of ISO8424 and 9689.
4.1 Water Resistance [RW(p)] and Acid Resistance [RA(p)] (Powder Method)
The glass to be tested is crushed to 425μm ~ 600μm grains. A sample of this powder equivalent to the specific gravity in grams is placed on a platinum basket. This is put in a flask of silica glass containing the reagent and boiled for 60 minutes. The sample is then carefully dried and re-weighed to determine the loss of weight (percent) and classified as per Tables 1 and 2. The reagent used for the water resistance test is distilled water (pH 6.5 ~ 7.5). 1/100N nitric acid is used for the acid resistance test.
Table1 Water Resistance
| Class | 1 | 2 | 3 | 4 | 5 | 6 |
| Loss of wt% | <0.05 | >0.05 <0.10 | >0.01 <0.25 | >0.25 <0.60 | >0.60 <1.10 | >1.10 |
Table2 Acid Resistance
| Class | 1 | 2 | 3 | 4 | 5 | 6 |
| Loss of wt% | <0.20 | >0.20 <0.35 | >0.35 <0.65 | 0.65> 1.2< | 1.20> 2.20< | 2.20> |
4.2 Weathering Resistance [W(s)] (Surface Method)
This test is carried out by putting freshly polished glass plates in a chamber at +50°C, 85% humidity for 24 hours. If the glass surface is severely attacked, another 6 hour test is carried out with new pieces. The classification into four groups is then obtained by inspecting the treated surface through a 50x microscope as per Table 3.
Table 3
| Class | Classification |
| 1 | When there is no fading on the glass exposed in the chamber for 24 hours and observed at 6000 luxes. |
| 2 | When there is no fading observed on the glass exposed in the chamber for 24 hours at 1500 luxes but fading is observed at 6000 luxes. |
| 3 | When fading is observed on the glass exposed in the chamber for 24 hours when inspected at 1500 luxes. |
| 4 | When fading is observed on the glass exposed in the chamber for 6 hours when inspected at 1500 luxes. |
4.3 lSO Method
4.3.1 Acid Resistance (SR)
Glass samples with dimensions of 30 x 30 x 2 mm are prepared. The surface of these samples are polished to the specified polishing conditions. They are hung by platinum wire into nitric acid solution (pH 0.3) or acetic acid buffer solution (pH 4.6) at 25degC for the length of times specified (10 minutes, 100 minutes, 16 hours or 100 hours). After this treatment, the loss of mass of the sample is determined using an analytical balance. Calculation of the time t0.1 in hours, necessary to etch a surface layer to a depth of 0.1μm is done using the following formula:
t 0.1= (tedS) / {(m1-m2)100}
0.1 : the time (h) necessary to etch a surface layer to a depth of0.1μm.
te :the time (h) for attack in the experiment
the specific gravity of the sample
S :the surface area (cm2 ) of the sample
m1 : the mass (mg) of the sample before the test
m2 : the mass (mg) of the sample after the test
The calculation is carried out by use of the value of the loss of mass which is ob-served by the minimum test condition (i.e., test solution and test time) for obtaining a loss of mass greater than 1 mg / sample. If the loss of mass is less than 1mg / sample after 100 hours exposure to pH 0.3, this value shall be accepted. The acid resistance class SR is obtained by comparison of the pH of the test solution and the time required for the attack to a depth of 0.1μm (h) with time scales given in the classification Table 4.
Table 4
Acid resistance class SR | 1 | 2 | 3 | 4 | 5 | 51 | 52 | 53 | |
| pH of the attacking solution | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 4.6 | 4.6 | 4.6 | 4.6 |
Time t0.1 needed to etch to a depth of 0.1μm (h) | >100 | 100 ~10 | 10 ~1 | 1 ~0.1 | <0.1 | >10 | 10 ~1 | 1 ~0.1 | <0.1 |
In addition, changes in the surface of the sample following the treatment are qualitatively evaluated with the naked eye. Additional classification numbers are given ac-cording to Table 5.
Table 5
| Additional Number | Changes in the Surface |
| .0 | No visible changes |
| .1 | Clear, but irregular surface (wavy, pockmarked) |
| .2 | Interference colors (slight selective leaching) |
| .3 | Tenacious thin whitish layer (stronger selective |
| .4 | Loosely adhering thick layer (Surface crust) |
4.3.2 Phosphate Resistance (PR)
Glass samples with dimensions of 30 x 30 x 2 mm are prepared and all surfaces are polished to given specifications. They are hung by platinum wire into aqueous solution containing 0.01 mol / l purified tripolyphosphate at 50degC for specified lengths of time (15 minutes, 1 hour, 4 hours or 16 hours). After this treatment, the loss of mass of the sample is determined using an analytical balance. Calculation of the time t0.1 necessary to etch a surface layer to a depth of 0.1μm is made using the same formula which is used for obtaining the acid resistance (SR) in the previous section. In this case, however, the time units are minutes. The calculation is carried out, as a rule, using the value of the loss of mass which is observed under the minimum test conditions (i.e., test solution and test time for obtaining a loss of mass greater than 1 mg / sample). The phosphate resistance class PR is obtained by comparison of the time required for the attack to a depth of 0.1μm (min) with time scales given in classification Table 6.
Table 6
| Phosphate resistance class PR | 1 | 2 | 3 | 4 |
Time t0.1 needed to etch to a depth of 0.1μm/min) | >240 | 240 ~60 | 60 ~15 | <15 |
Next, changes in the surface of the sample following the treatment are qualitatively evaluated with the naked eye. Additional classification numbers are given in addition to the class number according to Table 5used for obtaining the acid resistance (SR) in the previous section. For example, it is indicated that the phosphate resistance class is PR 2.0 for optical glass which needs 120 minutes for attack to a depth of 0.1μm , with no visible changes in the surface after the attack.