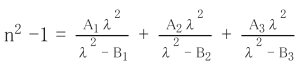5. Mechanical Properties
5.1 Modulus of Elasticity
Young’s modulus, Modulus of rigidity and Poisson’s ratio are determined by measuring the velocities of the longitudinal and transverse elastic waves in a well annealed rod of size 100 ~ 150 x 10 x 10 mm at room temperature. Young’s modulus (E), Modulus of rigidity (G) and Poisson’s ratio (s) are calculated using the following equations. Accuracy is ±1%.
Modulus of rigidity G = vt2p
Young’s Modulus E=(9KG)/(3K+G) vl : Velocity of longitudinal waves
Bulk Modulus K = v t2 p – (4/3)G vt : Velocity of transverse waves n: Density
Poisson’s ratio s=(E/2G)-1 p: Density
5.2 Knoop Hardness (Hk)
The indentation hardness of optical glass is determined with the aid of the micro hardness tester. One face of the specimen with the necessary thickness is polished. The diamond indentor is formed rhombic so that the vertically opposite angle from two axes is 172 °30′ and 130 ° respectively. The load time is 15 seconds, the load is 0.98 N. The glass specimen is indented at 5 places. Knoop hardness can be computed with the following equation:
Knoop Hardness =1.45l F/l2
F : Load (N) : l Length of longer diagonal line (mm)
Table 1 shows how the glasses are classified according to Knoop hardness. Please note the Knoop hardness figures have been rounded to the nearest 5 (e.g. value of 158 is shown as 160.)
Table 1
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Knoop Hardness | <150 | >150 250< | >250 350< | >350 450< | >> >450 550< | > 550 650< |
5.3 Abrasion (Aa)
A sample of size 30 x 30 x 10 mm is lapped on a 250 mm diameter cast iron flat, rotating at 60 rpm. The test piece is located 80 mm from the center of the flat and is under a 9.8N load. 20 ml of water containing 10 g of aluminous abrasive as the lapping material, with mean grain size 20µm(#800), is supplied evenly to the test piece for 5 minutes. The weight loss of the test piece is then measured. The known weight loss of the standard glass is compared according to the following equation:
Abrasion = {(Weight loss of sample / Specific gravity)/( Weight loss of standard sample / Specific gravity)} X 100
Glasses showing a higher value are less resistant to abrasion.
5.4 Photoelastic Constant (ß)
Optical glass is usually free of strain, but when mechanical or thermal stress is exerted upon it, glass shows birefringence. Stress F(Pa), optical path difference d (nm) and thickness of glass d(cm) have the follow-ing relationship:
d = ß d F
In this case, proportional constant ß is called the photoelastic constant. It is listed in this catalog at a unit of (nm/cm/105 Pa). The photoelastic constant is the material constant which will change by glass type. By using it, optical path difference can be computed from given stress. Internal stress can also be computed from optical path difference.