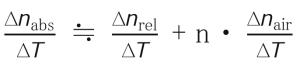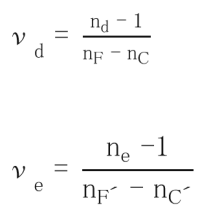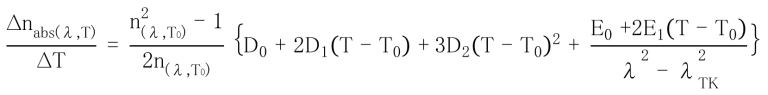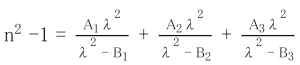Optical Properties
Optical Properties
2.1 Refractive Index
The refractive indices listed in this catalog were determined to the fifth decimal place for the following 20 lines of the spectrum. The refractive indices for d-line (587.56 nm) and e-line (546.07 nm) were determined to the sixth decimal place.
On the catalog pages, the wavelengths of each line are given in um units in parentheses under each spectrum line symbol.
Table1
| Spectral Line | t | ||||
| Light Source | Hg | Hg | Hg | Hg | Hg |
| Wavelength (nm) | 2325.42 | 1970.09 | 1529.58 | 1128.64 | 1013.98 |
| Spectral Line | s | A’ | r | C | C’ |
| Light Source | Cs | K | He | H | Cd |
| Wavelength (nm) | 852.11 | 768.19 | 706.52 | 656.27 | 643.85 |
| Spectral Line | He-Ne | D | d | e | F |
| Light Source | Laser | Na | He | Hg | H |
| Wavelength (nm) | 632.8 | 589.29 | 587.56 | 546.07 | 486.13 |
| Spectral Line | F’ | He-Cd | g | h | i |
| Light Source | Cd | Laser | Hg | Hg | Hg |
| Wavelength (nm) | 479.99 | 441.57 | 435.835 | 404.656 | 365.015 |
2.2 Dispersion
We have indicated (n F -n C ) and (n F´ -n C´ ) as the main dispersions. Abbe numbers were determined from the following vd and ve formula and calculated to the second decimal place:
vd = (n d -1)/(n F -n C ) ve =(n e -1)/(n F’ -n C’ )
We have also listed 12 partial dispersions (n x -n y ), 8 relative partial dispersions for the main dispersion (n F -n C ) and 4 for (n F´ -n C´ ). To make achromatization effective for more than two wavelengths, glasses which have favorable relationships between vd and the relative partial dispersion ө x,y for the wavelengths x and y are required. These may be defined as follows:
θ (x,y ) = ( n x -n y ) / (n F -n C )
2.3 Dispersion Formula
The refractive indices for wavelengths other than those listed in this catalog can be computed from a dispersion formula. As a practical dispersion formula, we have adopted the use of the Sellmeier formula shown below.
n² -1={A1 Λ² /(Λ² -B1 )} + {A² Λ² /(Λ² -B² )} + {A3 Λ² /(Λ² -B3 )}
The constants A1 ,A2 , A3 , B1 , B2 , B3 were computed by the method of least squares on the basis of refractive indices at standard wavelengths which were measured accurately from several melt samples. By using this formula, refractive indices for any wavelength between 365 and 2325nm can be calculated to have an accuracy of around ± 5 ×106. These constants A1 ,A2 , A3 , B1 , B2 , B3 are listed on the left side of the individual catalog pages. However in some glass types, not all refractive indices in the standard spectral range are listed on the data sheet. In such cases, the applicable scope of this dispersion formula is limited to the scope where refractive indices are given. When calculating a respective refractive index, please bear in mind that each wavelength is expressed in µm units.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
By using this website, you are hereby accepting the terms and conditions stipulated within the Privacy Policy Agreement. If you are not in agreement with our terms and conditions, then you should refrain from further use of our sites. In addition, your continued use of our website following the posting of any updates or changes to our terms and conditions shall mean that you agree and acceptance of such changes.
|
Temperature range (degC) |
dnair/dt (10-6/K) | ||||||
| t | C' | He-Ne | D | e | F' | g | |
| -40~-20 | -1.34 | -1.35 | -1.36 | -1.36 | -1.36 | -1.37 | -1.38 |
| -20~0 | -1.15 | -1.16 | -1.16 | -1.16 | -1.16 | -1.17 | -1.17 |
| 0~+20 | -0.99 | -1 | -1 | -1 | -1 | -1.01 | -1.01 |
| +20~+40 | -0.86 | -0.87 | -0.87 | -0.87 | -0.87 | -0.88 | -0.88 |
| +40~+60 | -0.763 | -0.77 | -0.77 | -0.77 | -0.77 | -0.77 | -0.78 |
| +60~+80 | -0.67 | -0.68 | -0.68 | -0.68 | -0.68 | -0.69 | -0.69 |
2.5 The refractive indices in Ultraviolet and the Infrared Range
The refractive indices in the ultraviolet and the infrared can be measured down to 157 nm in the ultraviolet and up to 2,325.42 nm in the infrared.
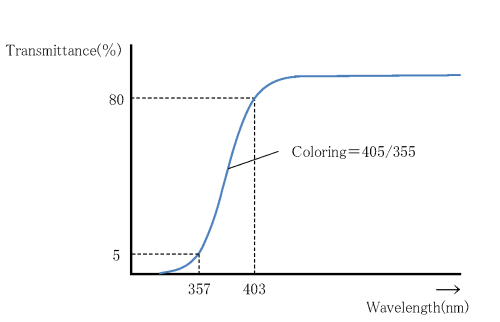
2.6 Internal Transmittance
Most types of Ohara optical glass are transparent and colorless because they are made of very pure materials. However, some optical glasses show remarkable absorption of light near the ultraviolet spectral range. For certain glasses with extreme optical properties, such as high refractive index, absorption extends to the visible range.
This not only depends on the chemical composition, but also on unavoidable impurities. In this catalog the internal transmittance is given – i.e., reflection losses are eliminated. Glass varies slightly from melt to melt and, therefore, listed are typical values of internal transmittance obtained on 10 mm thick samples chosen from many melts, measured from 280 nm to 2400 nm.
